Everything You Need to Know About Complex Numbers

Imaginary numbers always confused me. Like understanding e, virtually explanations fell into i of two categories:

• It's a mathematical abstraction, and the equations work out. Deal with it.
• Information technology's used in avant-garde physics, trust u.s.. Just wait until college.

Gee, what a not bad way to encourage math in kids! Today we'll assault this topic with our favorite tools:

• Focusing on relationships, not mechanical formulas.
• Seeing complex numbers as an upgrade to our number organisation, just like zero, decimals and negatives were.
• Using visual diagrams, not only text, to sympathise the thought.

And our undercover weapon: learning by analogy. Nosotros'll approach imaginary numbers by observing its ancestor, the negatives. Here's your guidebook:

It doesn't brand sense notwithstanding, only hang in there. By the cease nosotros'll hunt down i and put information technology in a headlock, instead of the reverse.

Video Walkthrough:

Really Understanding Negative Numbers

Negative numbers aren't like shooting fish in a barrel. Imagine you're a European mathematician in the 1700s. Yous have 3 and 4, and know you can write iv – 3 = ane. Simple.

But what about 3-iv? What, exactly, does that hateful? How tin can yous take 4 cows from 3? How could you have less than nothing?

Negatives were considered absurd, something that "darkened the very whole doctrines of the equations" (Francis Maseres, 1759). Yet today, it'd be absurd to think negatives aren't logical or useful. Try request your teacher whether negatives decadent the very foundations of math.

What happened? Nosotros invented a theoretical number that had useful properties. Negatives aren't something nosotros tin touch or hold, merely they depict certain relationships well (like debt). It was a useful fiction.

Rather than saying "I owe you thirty" and reading words to see if I'thou upwardly or downwards, I can write "-30" and know it means I'g in the hole. If I earn money and pay my debts (-30 + 100 = lxx), I tin tape the transaction easily. I take +70 later, which ways I'yard in the articulate.

The positive and negative signs automatically keep track of the direction — y'all don't need a judgement to depict the impact of each transaction. Math became easier, more elegant. Information technology didn't matter if negatives were "tangible" — they had useful properties, and we used them until they became everyday items. Today you'd call someone obscene names if they didn't "get" negatives.

But let's not be smug well-nigh the struggle: negative numbers were a huge mental shift. Fifty-fifty Euler, the genius who discovered e and much more than, didn't sympathise negatives as we do today. They were considered "meaningless" results (he later made up for this in fashion).

Information technology'due south a testament to our mental potential that today's children are expected to understand ideas that once confounded ancient mathematicians.

Enter Imaginary Numbers

Imaginary numbers have a similar story. We can solve equations like this all day long:

The answers are 3 and -three. Just suppose some wiseguy puts in a teensy, tiny minus sign:

Uh oh. This question makes most people blench the first time they see it. You lot want the foursquare root of a number less than zero? That's absurd! (Historically, there were real questions to answer, but I like to imagine a wiseguy.)

It seems crazy, merely similar negatives, zero, and irrationals (non-repeating numbers) must take seemed crazy at first. There'southward no "real" meaning to this question, right?

Incorrect. So-called "imaginary numbers" are as normal as every other number (or just as false): they're a tool to draw the earth. In the same spirit of assuming -1, .three, and 0 "exist", permit's assume some number i exists where:

That is, you multiply i by itself to go -1. What happens at present?

Well, first we get a headache. But playing the "Let's pretend i exists" game actually makes math easier and more elegant. New relationships emerge that we can describe with ease.

You may not believe in i, merely like those fuddy former mathematicians didn't believe in -1. New, encephalon-twisting concepts are hard and they don't make sense immediately, fifty-fifty for Euler. Simply as the negatives showed us, foreign concepts can still be useful.

I dislike the term "imaginary number" — it was considered an insult, a slur, designed to injure i's feelings. The number i is just as normal as other numbers, but the name "imaginary" stuck so nosotros'll use it.

Visual Understanding of Negative and Complex Numbers

As we saw last time, the equation $x^2 = 9$ really ways:

or

What transformation 10, when applied twice, turns ane to ix?

The two answers are "x = 3" and "ten = -3": That is, yous can "calibration by" 3 or "scale past three and flip" (flipping or taking the opposite is ane interpretation of multiplying by a negative).

Now let'south think about $x^2 = -ane$, which is actually

What transformation x, when applied twice, turns 1 into -1? Hrm.

• We can't multiply by a positive twice, because the result stays positive
• We can't multiply by a negative twice, because the result volition flip back to positive on the 2d multiplication

Merely what near… a rotation! It sounds crazy, but if we imagine x being a "rotation of xc degrees", then applying x twice will be a 180 degree rotation, or a flip from 1 to -one!

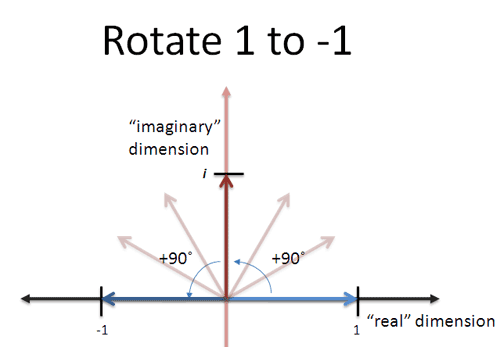
Yowza! And if we recollect about it more than, we could rotate twice in the other direction (clockwise) to plough 1 into -i. This is "negative" rotation or a multiplication by -i:

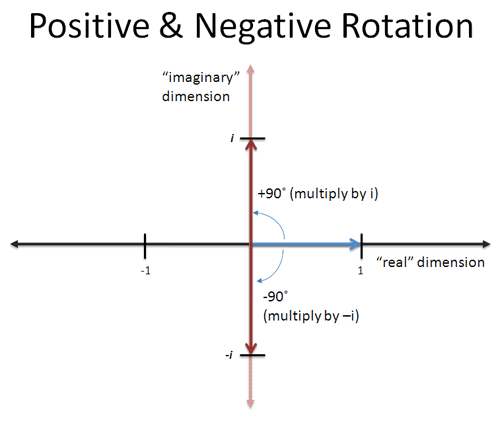
If we multiply by -i twice, the starting time multiplication would turn 1 into -i, and the second turns -i into -1. So there's actually two square roots of -1: i and -i.

This is pretty cool. Nosotros take some sort of answer, only what does it mean?

• i is a "new imaginary dimension" to measure a number
• i (or -i) is what numbers "become" when rotated
• Multiplying i is a rotation by 90 degrees counter-clockwise
• Multiplying past -i is a rotation of 90 degrees clockwise
• Two rotations in either direction is -1: it brings usa back into the "regular" dimensions of positive and negative numbers.

Numbers are 2-dimensional. Yes, it'south heed angle, just like decimals or long division would exist mind-bending to an ancient Roman. (What do you hateful there'southward a number betwixt one and 2?). It's a foreign, new way to recall about math.

We asked "How do nosotros turn ane into -ane in two steps?" and found an answer: rotate it 90 degrees. It's a strange, new way to think about math. Only it'south useful. (By the way, this geometric interpretation of complex numbers didn't get in until decades later on i was discovered).

Also, proceed in mind that having counter-clockwise be positive is a human convention — it hands could have been the other way.

Finding Patterns

Allow's dive into the details a bit. When multiplying negative numbers (like -1), yous become a pattern:

• 1, -1, 1, -one, i, -1, 1, -1

Since -1 doesn't change the size of a number, only the sign, you flip dorsum and along. For some number "x", you lot'd get:

• 10, -x, x, -10, ten, -ten…

This idea is useful. The number "x" can represent a expert or bad hair calendar week. Suppose weeks alternating between good and bad; this is a good week; what will it exist like in 47 weeks?

So -x means a bad hair week. Notice how negative numbers "proceed track of the sign": nosotros tin throw $(-one)^{47}$ into a calculator without having to count ("Week i is skillful, calendar week two is bad… week iii is good…"). Things that flip dorsum and forth tin be modeled well with negative numbers.

Ok. At present what happens if we go on multiplying past $i$?

Very funny. Allow's reduce this a chip:

• $1 = 1$ (No questions hither)
• $i = i$ (Tin can't do much)
• $i^ii = -1$ (That's what i is all almost)
• $i^iii = (i \cdot i) \cdot i = -1 \cdot i = -i$ (Ah, 3 rotations counter-clockwise = 1 rotation clockwise. Not bad.)
• $i^4 = (i \cdot i) \cdot (i \cdot i) = -1 \cdot -1 = i$ (4 rotations bring usa "full circle")
• $i^v = i^4 \cdot i = 1 \cdot i = i$ (Here nosotros go again…)

Represented visually:

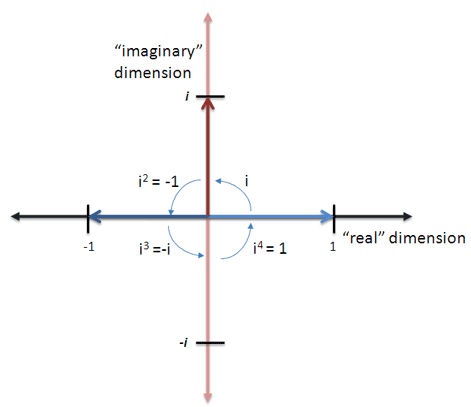
We bicycle every fourth rotation. This makes sense, right? Any kid tin can tell yous that 4 left turns is the same as no turns at all. At present rather than focusing on imaginary numbers ($i$, $i^2$), look at the general pattern:

• X, Y, -X, -Y, X, Y, -X, -Y…

Like negative numbers modeling flipping, imaginary numbers tin model annihilation that rotates between two dimensions "X" and "Y". Or anything with a circadian, round relationship — have anything in listen?

'Cos it'd exist a sin if you didn't. There'll de Moivre be more than in future articles. [Editor's note: Kalid is in electroshock therapy to treat his pun addiction.]

Understanding Circuitous Numbers

In that location's another item to cover: can a number exist both "real" and "imaginary"?

You lot bet. Who says we have to rotate the entire xc degrees? If nosotros go along ane foot in the "real" dimension and some other in the imaginary one, it looks like this:

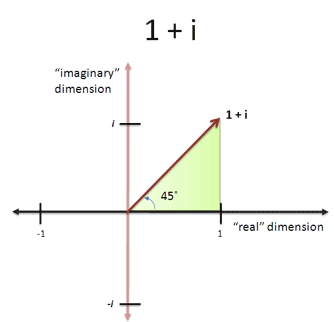
We're at a 45 degree angle, with equal parts in the real and imaginary (one + i). It'south like a hotdog with both mustard and ketchup — who says you demand to cull?

In fact, we can option whatsoever combination of real and imaginary numbers and brand a triangle. The angle becomes the "angle of rotation". A complex number is the fancy name for numbers with both real and imaginary parts. They're written a + bi, where

• a is the real office
• b is the imaginary part

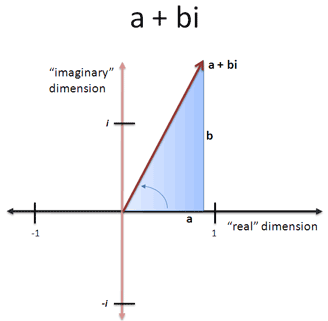
Not too bad. Merely in that location's 1 final question: how "big" is a complex number? We can't mensurate the real function or imaginary parts in isolation, because that would miss the large movie.

Let's step back. The size of a negative number is not whether you lot tin can count information technology — it'due south the altitude from zero. In the example of negatives this is:

Which is some other manner to find the absolute value. Just for complex numbers, how do nosotros measure two components at 90 degree angles?

It'due south a bird… it's a airplane… information technology's Pythagoras!

Geez, his theorem shows up everywhere, even in numbers invented 2000 years afterward his time. Yeah, we are making a triangle of sorts, and the hypotenuse is the distance from null:

Peachy. While measuring the size isn't equally easy as "dropping the negative sign", complex numbers do have their uses. Let's take a look.

A Real Example: Rotations

We're non going to wait until higher physics to use imaginary numbers. Permit's endeavor them out today. There's much more to say about complex multiplication, but keep this in mind:

• Multiplying by a complex number rotates by its angle

Let's have a await. Suppose I'k on a boat, with a heading of 3 units East for every 4 units N. I want to alter my heading 45 degrees counter-clockwise. What'south the new heading?

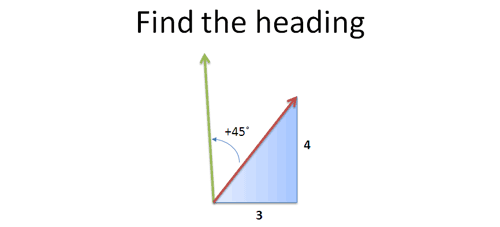
Some hotshot will say "That's simple! Only take the sine, cosine, gobbledegook past the tangent… fluxsom the foobar… and…". Crack . Sorry, did I break your calculator? Care to answer that question again?

Let'southward endeavor a simpler approach: nosotros're on a heading of 3 + 4i (whatever that angle is; we don't really intendance), and want to rotate by 45 degrees. Well, 45 degrees is one + i (perfect diagonal), so we tin can multiply past that amount!

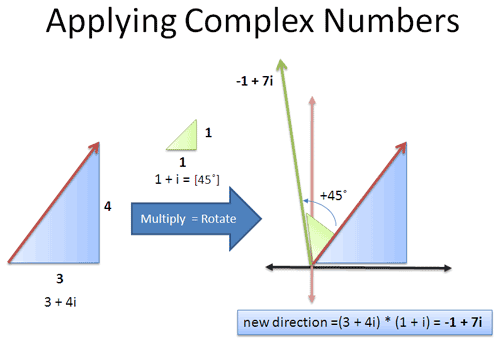
Here's the idea:

• Original heading: 3 units East, iv units North = three + 4i
• Rotate counter-clockwise by 45 degrees = multiply by 1 + i. (Hither's why multiplication, non addition, performs the rotation.)

If we multiply them together we get:

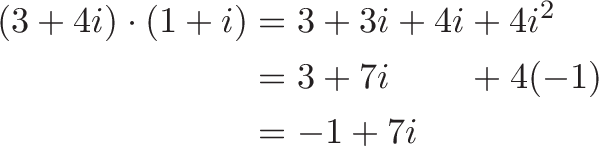
So our new orientation is one unit of measurement West (-1 East), and vii units North, which you could describe out and follow.

Simply yowza! Nosotros found that out in 10 seconds, without touching sine or cosine. At that place were no vectors, matrices, or keeping track what quadrant we are in. Information technology was just arithmetic with a touch of algebra to cross-multiply. Imaginary numbers take the rotation rules baked in: it just works.

Fifty-fifty better, the consequence is useful. Nosotros accept a heading (-ane, 7) instead of an angle (atan(7/-1) = 98.13, keeping in mind we're in quadrant ii). How, exactly, were y'all planning on drawing and following that bending? With the protractor you keep around?

No, you'd convert it into cosine and sine (-.14 and .99), find a reasonable ratio betwixt them (about i to 7), and sketch out the triangle. Complex numbers shell you to it, instantly, accurately, and without a figurer.

If you're like me, y'all'll discover this use mind-blowing. And if you don't, well, I'm afraid math doesn't toot your horn. Sorry.

Trigonometry is corking, just complex numbers can make ugly calculations uncomplicated (like computing cosine(a+b) ). This is simply a preview; later manufactures will give you the full meal.

Aside: Some people think "Hey, information technology's not useful to take North/Due east headings instead of a caste angle to follow!"

Actually? Ok, expect at your right manus. What's the angle from the bottom of your pinky to the tiptop of your index finger? Good luck figuring that out on your ain.

With a heading, you can at to the lowest degree say "Oh, information technology's X inches across and Y inches up" and take some chance of working with that begetting.

Complex Numbers Aren't

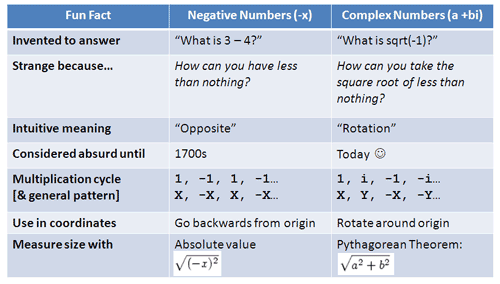
That was a cyclone tour of my bones insights. Take a look at the get-go chart — it should make sense at present.

There's so much more to these beautiful, zany numbers, but my brain is tired. My goals were uncomplicated:

• Convince you that complex numbers were considered "crazy" merely can be useful (just like negative numbers were)
• Show how complex numbers tin can brand certain problems easier, like rotations

If I seem hot and bothered virtually this topic, there'south a reason. Imaginary numbers have been a bee in my bonnet for years — the lack of an intuitive insight frustrated me.

Now that I've finally had insights, I'thousand bursting to share them. But it frustrates me that you're reading this on the blog of a wild-eyed lunatic, and not in a classroom. We suffocate our questions and "chug through" — because nosotros don't search for and share make clean, intuitive insights. Egad.

Just ameliorate to light a candle than curse the darkness: hither's my thoughts, and one of you volition smoothen a spotlight. Thinking we've "figured out" a topic similar numbers is what keeps us in Roman Numeral land.

In that location's much more circuitous numbers: check out the details of complex arithmetic. Happy math.

Epilogue: Only they're still strange!

I know, they're still strange to me too. I try to put myself in the heed of the first person to discover zip.

Nothing is such a weird idea, having "something" stand for "nothing", and information technology eluded the Romans. Complex numbers are similar — it's a new style of thinking. But both zero and circuitous numbers make math much easier. If nosotros never adopted strange, new number systems, nosotros'd still be counting on our fingers.

I repeat this illustration because it's so easy to starting time thinking that complex numbers aren't "normal". Allow's proceed our mind open: in the time to come they'll chuckle that complex numbers were in one case distrusted, even until the 2000'south.

If you want more nitty-gritty, check out wikipedia, the Dr. Math discussion, or another argument on why imaginary numbers exist.

Other Posts In This Series

1. A Visual, Intuitive Guide to Imaginary Numbers
2. Intuitive Arithmetic With Complex Numbers
3. Understanding Why Complex Multiplication Works
4. Intuitive Guide to Angles, Degrees and Radians
5. Intuitive Understanding Of Euler's Formula
6. An Interactive Guide To The Fourier Transform
7. Intuitive Guide to Convolution
8. Intuitive Understanding of Sine Waves
9. An Intuitive Guide to Linear Algebra
10. A Programmer'south Intuition for Matrix Multiplication
11. Imaginary Multiplication vs. Imaginary Exponents
12. Intuitive Guide to Hyperbolic Functions

kistlerpaboul.blogspot.com

Source: https://betterexplained.com/articles/a-visual-intuitive-guide-to-imaginary-numbers/

Share this post